As the development of new classes of antibiotics slows, bacterial resistance to existing drugs is becoming an increasing problem, with many fearing the advent of a post-antibiotic era. To counter this threat, we are developing a two-pronged attack: using a novel treatment strategy, guided by mathematical modelling.
Antibiotics act directly upon bacteria, either killing them or inhibiting their growth. Within any population of bacteria some will be susceptible to a chosen antibiotic, whilst others may exhibit varying degrees of resistance.
Therefore, antibiotics exert a ‘selective pressure’ upon bacteria, favouring the resistant strains, such that they become dominant in the population. If bacteria become resistant to a particular type of antibiotic, then an alternative variety may be used. In many cases this will clear an infection, in others the bacteria become resistant to this second treatment. At this point the bacteria are said to be multidrug resistant, and are often referred to as ‘superbugs’.
The danger is that bacterial infections may develop resistance to all available antibiotics, rendering them untreatable. As we begin to lose this arms race, it is imperative that we open up the battle on other fronts, developing alternative treatments and using them as effectively as possible.
We are building mathematical models to optimise the treatment of bacterial infections, using a new therapy developed by our collaborators in the Krachler Lab, here at the University of Birmingham.
In order for bacteria to gain a foothold in a host, they must bind to the host cells. This both protects them from mechanical clearance and assault by immune cells, and allows them to deploy an arsenal of so called ‘virulence mechanisms’, which reprogram the host cells to facilitate infection.
Dr Krachler has developed a new molecule, called MAM7, which binds to host cells, preventing the invading bacteria from doing likewise. In theory, this treatment should exert no selective pressure upon the bacteria, since any adaptation would merely result in them binding less effectively to host cells. Bacteria may then be cleared from the body by a combination of mechanical forces, the immune system and antibiotics.
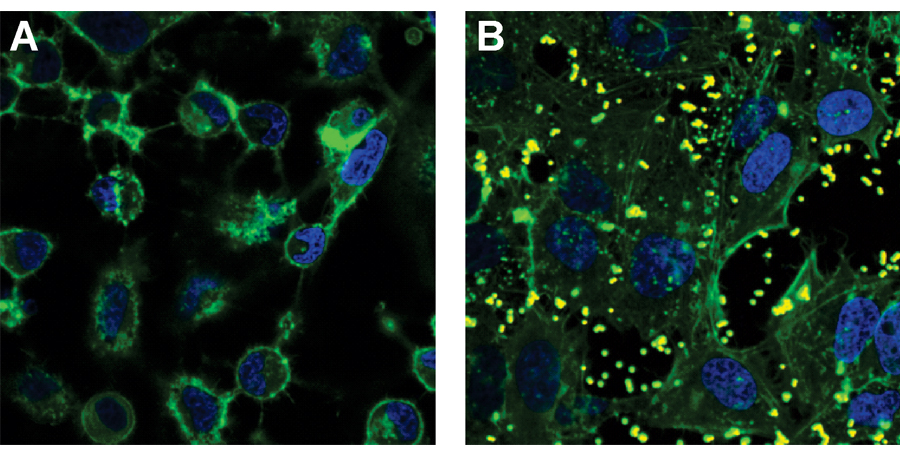Treatment of epithelial cells using MAM7. The green staining shows the skeletons of the cells and the blue staining shows the DNA-containing nuclei. A) untreated cells. B) cells treated with beads coated in MAM7 (beads are seen as yellow blobs). Figure reproduced, with permission, from Krachler et al. (2012).
Mathematical models may be used to determine the optimum treatment regimen, ensuring that bacteria are cleared as quickly as possible, whilst minimising the risk that resistance develops.
Mathematics enables us to extend the reach of experimental and clinical studies in at least three ways. Firstly, it allows us to understand and predict the behaviour of inherently ‘nonlinear’ biological systems. These nonlinearities are caused by feedback within the system.
For example, a nonlinear system could be represented as follows: A➝B➝C➝A, where the letters represent components in the system and the arrows represent effects exerted by one component upon another. In this case A feeds back on itself via B and C.
Secondly, it enables us to manipulate the system in ways that may not be possible experimentally. In this way we may evaluate the relative importance and effect of each component. For example, we could vary the rate of exchange of genes coding for antibiotic resistance between bacteria, to test the effect this has upon the size of the bacterial population over time. Lastly, it enables us to consider a wider range of scenarios and hypotheses than would be experimentally feasible, due to time, space or financial limitations.
Thus, theoretical modelling complements experimental studies, forming an experiment/modelling cycle: models are used to test biological hypotheses, and may then be used to make predictions which can be tested experimentally.
It is hoped that this study will help us to keep a step ahead in the fight against bacterial infections. A fight that it is critical we win.